Programación dinámica: ejemplos, problemas comunes y soluciones
No hay duda de que los problemas de programación dinámica pueden ser muy intimidantes en una entrevista de codificación. Incluso cuando sepa que un problema debe resolverse mediante un método de programación dinámica, es un desafío poder encontrar una solución que funcione en un período de tiempo limitado.
La mejor manera de ser bueno en los problemas de programación dinámica es revisar todos los que pueda. Si bien no es necesario que memorice la solución a cada problema, es bueno tener una idea de cómo implementar uno.
¿Qué es la programación dinámica?
En pocas palabras, la programación dinámica es un método de optimización para algoritmos recursivos, la mayoría de los cuales se utilizan para resolver problemas informáticos o matemáticos.
También puede llamarlo una técnica algorítmica para resolver un problema de optimización dividiéndolo en subproblemas más simples. Un principio clave en el que se basa la programación dinámica es que la solución óptima a un problema depende de las soluciones a sus subproblemas.
Siempre que veamos una solución recursiva que tiene llamadas repetidas para las mismas entradas, podemos optimizarla mediante programación dinámica. La idea es simplemente almacenar los resultados de los subproblemas para que no tengamos que volver a calcularlos cuando sea necesario más adelante.
Las soluciones programadas dinámicamente tienen una complejidad polinomial que asegura un tiempo de ejecución mucho más rápido que otras técnicas como la recursividad o el retroceso. En la mayoría de los casos, la programación dinámica reduce la complejidad del tiempo, también conocida como big-O , de exponencial a polinomial.
Ahora que tiene una buena idea de lo que es la programación dinámica, es hora de revisar algunos problemas comunes y sus soluciones.
Problemas de programación dinámica
1. Problema de la mochila
Planteamiento del problema
Dado un conjunto de artículos, cada uno con un peso y un valor, determine el número de cada artículo para incluir en una colección para que el peso total no exceda un límite dado y el valor total sea lo más grande posible.
Se le dan dos valores de matrices enteras [0..n-1] y pesos [0..n-1] que representan valores y pesos asociados con n elementos respectivamente. También se da un número entero W que representa la capacidad de la mochila.
Aquí estamos resolviendo el problema de la mochila 0/1, lo que significa que podemos optar por agregar un artículo o excluirlo.
Algoritmo
- Cree una matriz bidimensional con n + 1 filas y w + 1 columnas. Un número de fila n denota el conjunto de artículos de 1 a i , y un número de columna w denota la capacidad máxima de carga de la bolsa.
- El valor numérico en [i] [j] denota el valor total de los artículos hasta i en una bolsa que puede llevar un peso máximo de j.
- En cada coordenada [i] [j] de la matriz, elija el valor máximo que podemos obtener sin el elemento i , o el valor máximo que podemos obtener con el elemento i — el que sea mayor.
- El valor máximo que se puede obtener al incluir el artículo i es la suma del artículo i mismo y el valor máximo que se puede obtener con la capacidad restante de la mochila.
- Realice este paso hasta que encuentre el valor máximo para el W ª fila.
Código
def FindMax(W, n, values, weights):
MaxVals = [[0 for x in range(W + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
MaxVals[i][w] = 0
elif weights[i-1] <= w:
MaxVals[i][w] = max(values[i-1]
+ MaxVals[i-1][w-weights[i-1]],
MaxVals[i-1][w])
else:
MaxVals[i][w] = MaxVals[i-1][w]
return MaxVals[n][W]
2. Problema de cambio de moneda
Planteamiento del problema
Suponga que le dan una matriz de números que representan los valores de cada moneda. Dada una cantidad específica, encuentre la cantidad mínima de monedas que se necesitan para hacer esa cantidad.

Algoritmo
- Inicialice una matriz de tamaño n + 1 , donde n es la cantidad. Inicialice el valor de cada índice i en la matriz para que sea igual a la cantidad. Esto denota el número máximo de monedas (utilizando monedas de denominación 1) necesarias para completar esa cantidad.
- Como no hay denominación para 0, inicialice el caso base donde matriz [0] = 0 .
- Para cualquier otro índice i , comparamos el valor en él (que inicialmente se establece en n + 1 ) con la matriz de valores [ik] +1 , donde k es menor que i . Básicamente, esto verifica toda la matriz hasta i-1 para encontrar el número mínimo posible de monedas que podemos usar.
- Si el valor en cualquier matriz [ik] + 1 es menor que el valor existente en la matriz [i] , reemplace el valor en la matriz [i] con el de la matriz [ik] +1 .
Código
def coin_change(d, amount, k):
numbers = [0]*(amount+1)
for j in range(1, amount+1):
minimum = amount
for i in range(1, k+1):
if(j >= d[i]):
minimum = min(minimum, 1 + numbers[jd[i]])
numbers[j] = minimum
return numbers[amount]
3. Fibonacci
Planteamiento del problema
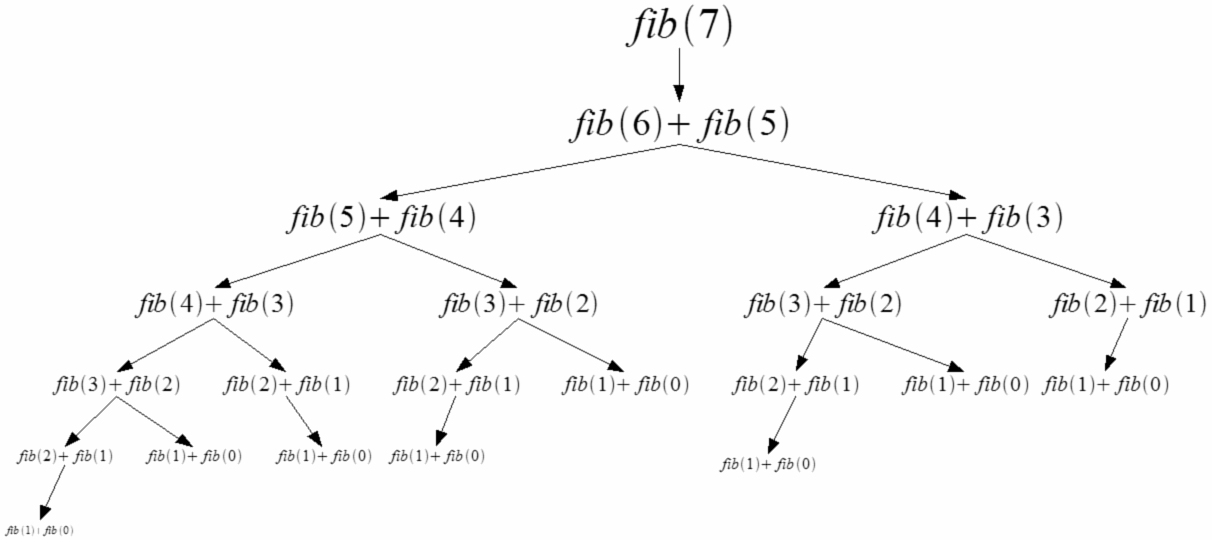
La serie de Fibonacci es una secuencia de números enteros donde el siguiente entero de la serie es la suma de los dos anteriores.
Está definido por la siguiente relación recursiva: F (0) = 0, F (n) = F (n-1) + F (n-2) , donde F (n) es el enésimo término. En este problema, tenemos que generar todos los números en una secuencia de Fibonacci hasta un enésimo término dado.
Algoritmo
- Primero, use un enfoque recursivo para implementar la relación de recurrencia dada.
- Resolver este problema de forma recursiva implica descomponer F (n) en F (n-1) + F (n-2) , y luego llamar a la función con F (n-1) y F (n + 2) como parámetros. Hacemos esto hasta que se alcanzan los casos base donde n = 0 , o n = 1 .
- Ahora, usamos una técnica llamada memorización. Almacene los resultados de todas las llamadas a funciones en una matriz. Esto asegurará que para cada n, F (n) solo necesita calcularse una vez.
- Para cualquier cálculo posterior, su valor simplemente se puede recuperar de la matriz en tiempo constante.
Código
def fibonacci(n):
fibNums = [0, 1]
for i in range(2, n+1):
fibNums.append(fibNums[i-1] + fibNums[i-2])
return fibNums[n]4. Subsecuencia creciente más larga
Planteamiento del problema
Encuentre la longitud de la subsecuencia creciente más larga dentro de una matriz dada. La subsecuencia creciente más larga es una subsecuencia dentro de una matriz de números con un orden creciente. Los números dentro de la subsecuencia deben ser únicos y en orden ascendente.
Además, los elementos de la secuencia no necesitan ser consecutivos.
Algoritmo
- Comience con un enfoque recursivo en el que calcule el valor de la subsecuencia creciente más larga de cada submatriz posible desde el índice cero hasta el índice i, donde i es menor o igual que el tamaño de la matriz.
- Para convertir este método en uno dinámico, cree una matriz para almacenar el valor de cada subsecuencia. Inicialice todos los valores de esta matriz a 0.
- Cada índice i de esta matriz corresponde a la longitud de la subsecuencia creciente más larga para una submatriz de tamaño i .
- Ahora, para cada llamada recursiva de findLIS (arr, n) , verifique el n- ésimo índice de la matriz. Si este valor es 0, a continuación, calcular el valor usando el método en el primer paso y almacenarla en el n-ésimo índice.
- Finalmente, devuelva el valor máximo de la matriz. Ésta es la longitud de la subsecuencia creciente más larga de un tamaño dado n .
Código
def findLIS(myArray):
n = len(myArray)
lis = [0]*n
for i in range (1 , n):
for j in range(0 , i):
if myArray[i] > myArray[j] and lis[i]< lis[j] + 1 :
lis[i] = lis[j]+1
maxVal= 0
for i in range(n):
maxVal = max(maxVal , lis[i])
return maxValSoluciones a problemas de programación dinámica
Ahora que ha pasado por algunos de los problemas de programación dinámica más populares, es hora de intentar implementar las soluciones usted mismo. Si está atascado, siempre puede volver y consultar la sección de algoritmos para cada problema anterior.
Dado lo populares que son hoy en día técnicas como la recursividad y la programación dinámica, no estará de más consultar algunas plataformas populares donde puede aprender dichos conceptos y perfeccionar sus habilidades de codificación . Si bien es posible que no se encuentre con estos problemas a diario, seguramente los encontrará en una entrevista técnica.
Naturalmente, tener el conocimiento de problemas comunes seguramente pagará dividendos cuando vaya a su próxima entrevista. ¡Así que abre tu IDE favorito y empieza!
