¿Qué es la recursividad y cómo se usa?
La recursividad es un concepto de programación divertido, pero puede ser un poco complicado de aprender. La recursividad simplemente significa algo que se repite. Si desea ver un ejemplo descarado de recursividad, intente buscar recursividad en Google. Encontrará un huevo de Pascua donde las sugerencias de resultados de búsqueda son recursivas. Si, por otro lado, desea aprender a codificar una función recursiva, ¡siga leyendo!
¿Qué es una función recursiva?
Una función recursiva es una función que se llama a sí misma. Básicamente, creas un bucle con una función. Como puede imaginar, estas pueden ser funciones difíciles de escribir. No desea que su código se ejecute para siempre.
Similar a un ciclo, una función recursiva será controlada por una condición. Una vez que se cumple la condición, la función deja de llamarse a sí misma, lo que detiene el ciclo. Así es como puede crear una función que se llame a sí misma sin que se ejecute para siempre.
Aunque una función recursiva actúa como un bucle, la computadora la ejecuta de manera diferente. Entonces, algunos algoritmos son más eficientes en un bucle y otros se benefician de una función recursiva. Pero antes de ver cómo usar una función recursiva, necesita saber cómo escribir una.
Cómo escribir una función recursiva
Todas las funciones recursivas tienen la misma estructura básica:
FUNCTION name
IF condition THEN
RETURN result
ELSE
CALL FUNCTION name
END FUNCTIONEl ejemplo anterior está escrito en pseudocódigo. Describe la estructura de la función, que se puede aplicar a cualquier idioma. Para simplificar, en este artículo nos concentraremos en Python.
Lo primero que se debe tener en cuenta sobre una función recursiva es que cuando se cumple la condición, la función sale de la recursividad. Esto significa que cuando escribe una función recursiva, lo primero que querrá determinar es cuándo detener la recursividad.
Si no se cumple la condición, la función se llamará a sí misma. Entonces, si desea enviar información al siguiente bucle, deberá enviarla como un argumento en su función. Esto puede dar a las funciones recursivas mucho más poder.
Ejemplo de función recursiva en Python
Será mucho más fácil entender cómo funciona la recursividad cuando la vea en acción. Para demostrarlo, escribamos una función recursiva que devuelva el factorial de un número.
Los factoriales devuelven el producto de un número y de todos los enteros anteriores. Por ejemplo, el factorial de 5 es 5 x 4 x 3 x 2 x 1 o 120.
def factorialFunction(numberToMultiply):
if numberToMultiply == 1 :
return 1
else :
return numberToMultiply * factorialFunction(numberToMultiply - 1)
result = factorialFunction(3)
print(result)
//Outputs: 6
El programa anterior le dará el resultado 6, que es el factorial del número 3. Esto puede ser un poco confuso al principio. Ayudará si ejecutamos el programa paso a paso.
- Cuando se llama a la función, numberToMultiply es igual a 3.
- La condición no se cumple, así que pasamos a la condición else .
- Nuestra función devuelve 3 * pero luego se pausa. Debe llamarse a sí mismo para determinar el resto del valor que está devolviendo.
- Cuando se llama a la función esta vez, el valor de numberToMultiply es igual a 2.
- La condición no se cumple, así que pasamos a la condición else.
- Nuestra función devuelve 2 * pero luego se pausa. Debe llamarse a sí mismo para determinar el resto del valor que está devolviendo.
- La función se llama una vez más. Esta vez, el valor de numberToMultiply es igual a 1.
- Nuestra condición si se cumple. La función devuelve 1.
- La función del paso 6 ahora puede devolver 2 * 1 a la función del paso 3.
- La función en el paso tres ahora puede devolver 3 * 2 * 1, que es 6.
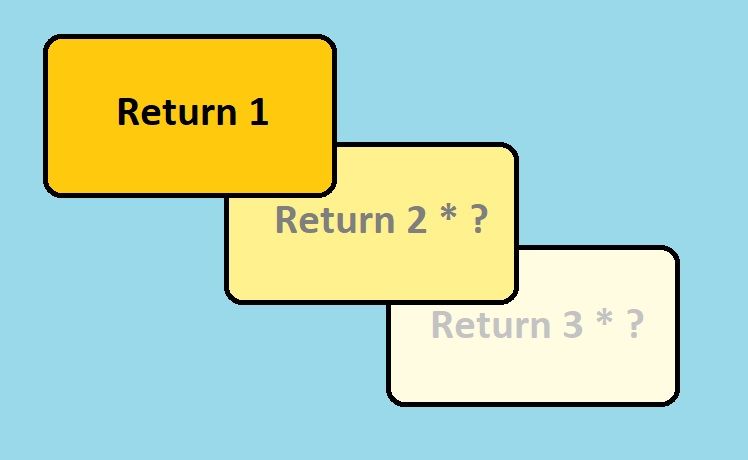
La recursividad es un concepto complicado. Puede ser útil pensar en ello como apilar una función sobre otra función. Una vez que una función se resuelve finalmente, puede enviar la información de vuelta a la pila, hasta que todas las funciones tengan su respuesta.
En realidad, esto es lo que hace tu computadora. Cuando llama a la función, se mantiene en la memoria hasta que se devuelve. Esto significa que las funciones recursivas pueden usar mucha más memoria que un bucle.
Por lo tanto, puede que no sea eficiente escribir bucles como funciones recursivas, pero es una excelente manera de practicar su construcción. Debería poder codificar bucles como funciones recursivas con resultados similares.
Un ejemplo de cómo convertir un bucle en una función recursiva
print("Enter an even number:")
i = int(input())
while (i % 2) != 0 :
print("That number is not even. Please enter a new number:")
i = int(input())Este bucle también se puede escribir de forma recursiva como:
def recursiveFunction(number) :
if (number % 2) == 0 :
return number
else:
print("That number is not even. Please enter a new number:")
recursiveFunction(int(input()))
print("Enter and even number:")
i = recursiveFunction(int(input()))El primer paso es determinar cuándo desea que se detenga su función. En este caso, queremos que se detenga una vez que se ingrese un número par. En nuestro ejemplo, el número rastrea la entrada del usuario. Si ingresan un número par, devolvemos el número. De lo contrario, continuaremos solicitando un nuevo número.
Para configurar el ciclo, volvemos a llamar a nuestra función. Pero esta vez, el número que pasamos a la siguiente función es el nuevo número introducido por el usuario. La siguiente llamada de función comprobará el número.
¡Esta es una función realmente mala! Sí, está comprobando si el número es par, como nuestro ciclo, pero no es eficiente. Cada vez que el usuario ingresa un número impar, la función se guarda en la memoria y se llama a una nueva función. Si haces esto suficientes veces, ¡te quedarás sin memoria!
Un ejemplo del mundo real de una función recursiva
Los ejemplos anteriores son buenos ejemplos de cuándo no utilizar la recursividad. Entonces, ¿dónde se usa la recursividad? Un buen ejemplo de cuándo querría usar la recursividad es buscar en un árbol binario.
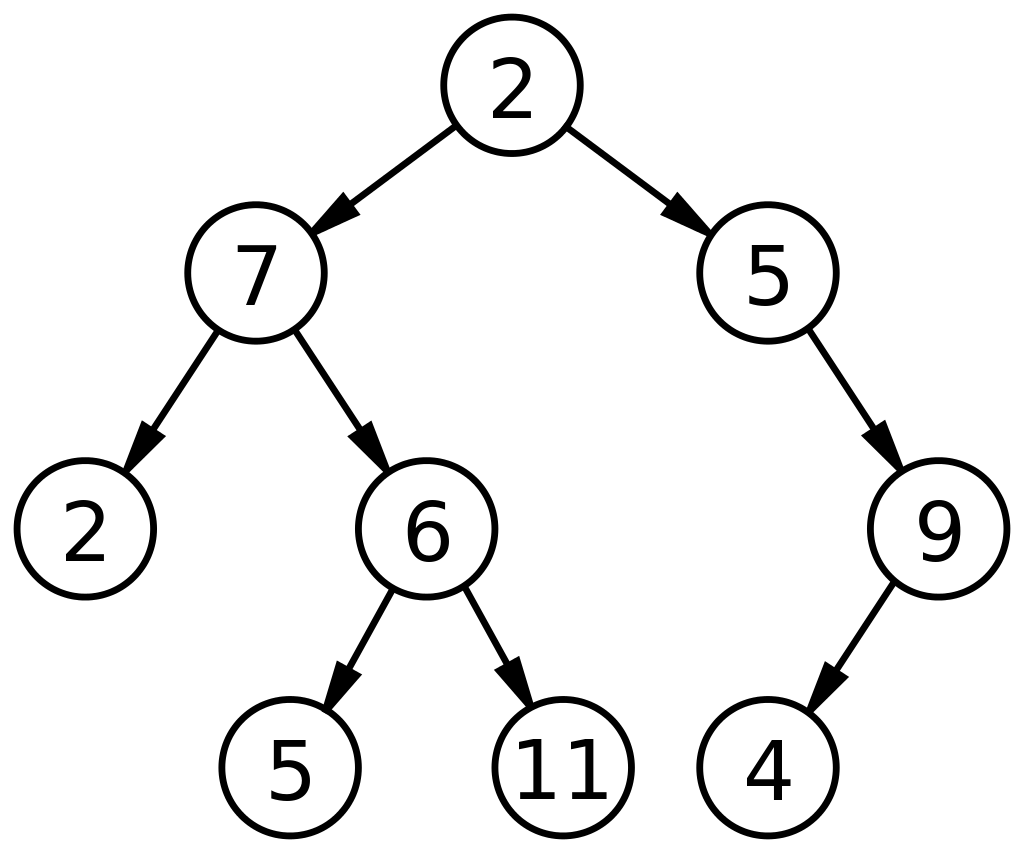
Cuando los datos están estructurados en un árbol binario, debe recorrer muchas rutas para buscar datos. En cada punto del árbol, debe decidir si desea continuar buscando a la derecha o a la izquierda. Puede guardar qué parte del árbol visitó en una variable, pero una función recursiva naturalmente puede rastrear esa información.
Imagina que estamos buscando el número seis en el árbol de arriba. Podríamos hacer una función recursiva que busque en el árbol de izquierda a derecha. El algoritmo se vería así:
FUNCTION searchTree(branchToSearch)
IF find 6 OR end of tree THEN
RETURN result
ELSE
PROCESS branch
CALL FUNCTION searchTree(left)
CALL FUNCTION searchTree(right)
END FUNCTIONEn este ejemplo de pseudocódigo, el algoritmo buscaría primero en el lado izquierdo del árbol. Cada vez que visita un número nuevo, la función se detiene y se guarda en la memoria. Esto nos permite rastrear dónde hemos estado.
El algoritmo siempre buscará primero en el lado izquierdo tanto como pueda. una vez que llega al final del árbol, el árbol de búsqueda (izquierda) se completará y comprobará el lado derecho. Una vez que se verifican ambos lados, la búsqueda retrocede una rama y continúa verificando el lado derecho.
Si los algoritmos buscaran en todo el árbol, lo harían en el orden:
2, 7, 2, 6, 5, 11, 5, 9 y 4
Vea si puede seguir usando el pseudocódigo anterior.
Revisión de la recursividad
La recursividad es un tema avanzado. Llevará algún tiempo comprenderlo y aún más aprender a codificarlo. Le ayudará si recorre las funciones recursivas paso a paso. Incluso podría ser útil apilar tarjetas de índice o notas adhesivas a medida que avanza en una función cuando aprende a representar cada llamada de función.
Al escribir una función recursiva, comience por decidir cómo desea salir de la función. A continuación, determine cómo configurar su bucle. Identifique qué información debe enviarse a la siguiente llamada de función y qué debe devolverse.
La mejor forma de aprender la recursividad es practicarla y aprender de tus errores. Mire algunos de sus códigos antiguos y desafíese a reescribir los bucles como funciones recursivas. Probablemente no hará que su código sea más eficiente, pero será una buena práctica.
