Cómo utilizar la clasificación por selección

La clasificación por selección es una técnica de clasificación que selecciona un elemento de la lista y luego cambia su lugar por otro. Selecciona el elemento más grande y luego lo intercambia con un elemento en el índice más alto de la lista.

El algoritmo hace esto repetidamente hasta que se ordena la lista. Si no está seguro de cómo funciona el ordenamiento por selección, ha venido al lugar correcto. Lo explicaremos con más profundidad a continuación, además de mostrarte un ejemplo.

Orden de selección: un vistazo más de cerca

Suponga que tiene la lista: [39, 82, 2, 51, 30, 42, 7]. Para ordenar la lista usando la ordenación por selección, primero tendría que encontrar el número más alto en ella.

Con la lista dada, ese número es 82. Cambie 82 por el número en el índice más alto (es decir, 7).

Después de la primera pasada, el nuevo orden de la lista será: [39, 7, 2, 51, 30, 42, 82]. Cada vez que el algoritmo revisa toda la lista, eso se denomina "pase".

Observe que la lista mantiene una sublista ordenada y una sublista sin clasificar durante el proceso de clasificación.

Relacionado: ¿Qué es la notación Big-O?

La lista original comienza con una lista ordenada de cero elementos y una lista sin ordenar de todos los elementos. Luego, después de la primera pasada, tiene una lista ordenada que solo tiene el número 82.

En la segunda pasada, el número más alto en la sublista sin clasificar será 51. Este número se intercambiará con 42 para dar el orden de la nueva lista a continuación:

[39, 7, 2, 42, 30, 51, 82].

El proceso se repite hasta que se ordena toda la lista. La siguiente figura resume todo el proceso:

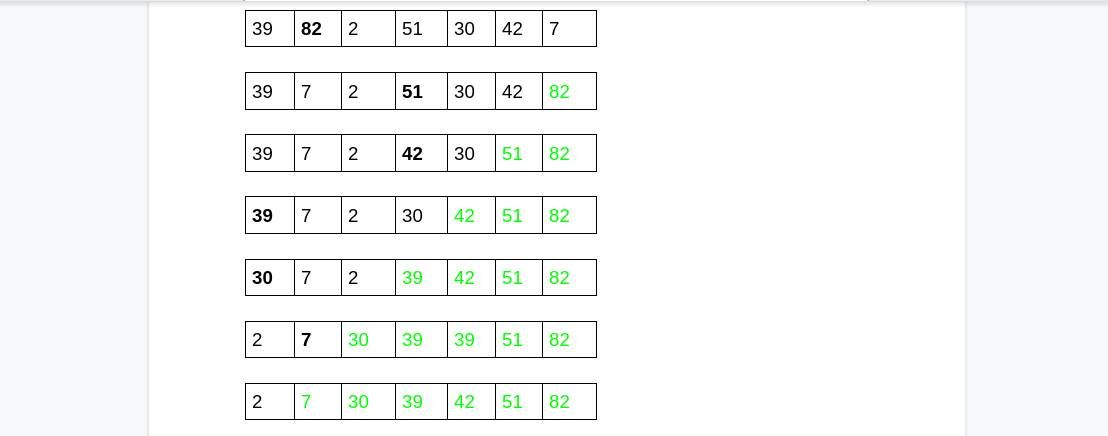
Los números en negrita muestran el valor de lista más alto en ese momento. Los que están en verde muestran la sublista ordenada.

Análisis de algoritmos

Para obtener la complejidad (usando la notación Big-O) de este algoritmo, siga a continuación:

En la primera pasada, se hacen (n-1) comparaciones. En la segunda pasada, (n-2). En la tercera pasada, (n-3) y así sucesivamente hasta la (n-1) ésima pasada que hace solo una comparación.

Resumiendo las comparaciones de la siguiente manera, se obtiene:

(n-1) + (n-1) + (n-1) + … + 1 = ((n-1) n) / 2.

Por lo tanto, el ordenamiento por selección es O (n ² ).

Implementación de código

El código muestra funciones que puede utilizar para realizar la ordenación por selección utilizando Python y Java.

Pitón:

 def selectionSort(mylist):
 for x in range(len(mylist) - 1, 0, -1):
 max_idx = 0
 for posn in range(1, x + 1):
 if mylist[posn] > mylist[max_idx]:
 max_idx = posn
 temp = mylist[x]
 mylist[x] = mylist[max_idx]
 mylist[max_idx] = temp

Java:

 void selectionSort(int my_array[]){
 for (int x = 0; x < my_array.length - 1; x++)
 {
 int index = x;
 for (int y = x + 1; y < my_array.length; y++){
 if (my_array[y] < my_array[index]){
 index = y; // find lowest index
 }
 }
 int temp = my_array[index]; // temp is a temporary storage
 my_array[index] = my_array[x];
 my_array[x] = temp;
 }}

Pasar de la clasificación por selección a la clasificación por fusión

Como ha mostrado el análisis del algoritmo anterior, el algoritmo de clasificación de selección es O (n ² ). Tiene una complejidad exponencial y, por lo tanto, es ineficaz para conjuntos de datos muy grandes.

Un algoritmo mucho mejor para usar sería el tipo de combinación con una complejidad de O (nlogn). Y ahora que sabe cómo funciona el ordenamiento por selección, el siguiente paso en su lista de estudio para los algoritmos de ordenamiento debería ser el ordenamiento por combinación.