7 algoritmos que todo programador debe conocer
Como estudiante de programación, es probable que haya aprendido muchos algoritmos diferentes a lo largo de su carrera. Dominar diferentes algoritmos es absolutamente esencial para cualquier programador.
Con tantos algoritmos, puede resultar difícil realizar un seguimiento de lo que es esencial. Si se está preparando para una entrevista o simplemente está mejorando sus habilidades, esta lista lo hará relativamente fácil. Siga leyendo mientras enumeramos los algoritmos más esenciales para los programadores.
1. Algoritmo de Dijkstra
Edsger Dijkstra fue uno de los científicos informáticos más influyentes de su tiempo y contribuyó en muchas áreas diferentes de la ciencia de la computación, incluidos los sistemas operativos, la construcción de compiladores y mucho más. Una de las contribuciones más notables de Dijkstra es el ingenio de su algoritmo de ruta más corta para gráficos, también conocido como el algoritmo de ruta más corta de Dijkstra.
El algoritmo de Dijkstra encuentra la ruta más corta en un gráfico desde una fuente hasta todos los vértices del gráfico. En cada iteración del algoritmo, se agrega un vértice con la distancia mínima desde la fuente y uno que no existe en la ruta más corta actual. Esta es la propiedad codiciosa utilizada por el algoritmo de Djikstra.
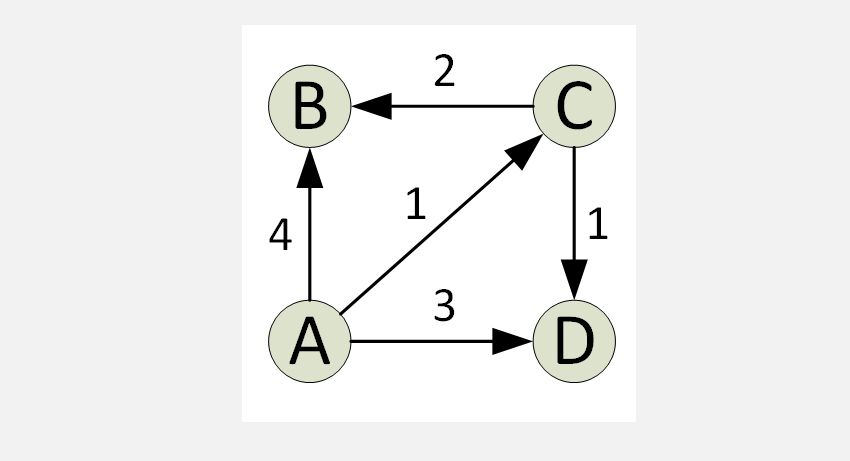
El algoritmo se implementa normalmente mediante un conjunto. El algoritmo de Dijkstra es muy eficiente cuando se implementa con un Min Heap; puede encontrar el camino más corto en solo O (V + ElogV) tiempo (V es el número de vértices y E es el número de aristas en un gráfico dado).
El algoritmo de Dijkstra tiene sus limitaciones; solo funciona en gráficos dirigidos y no dirigidos con bordes de peso positivo. Para pesos negativos, generalmente es preferible el algoritmo de Bellman-Ford.
Las preguntas de la entrevista suelen incluir el algoritmo de Djikstra, por lo que recomendamos encarecidamente comprender sus intrincados detalles y aplicaciones.
2. Combinar ordenación
Tenemos un par de algoritmos de clasificación en esta lista, y la clasificación por fusión es uno de los algoritmos más importantes. Es un algoritmo de clasificación eficiente basado en la técnica de programación Divide and Conquer. En el peor de los casos, la ordenación por combinación puede ordenar "n" números en solo O (nlogn) tiempo. En comparación con las técnicas de clasificación primitivas como Bubble Sort (que lleva O (n ^ 2) tiempo), la clasificación por fusión es excelentemente eficiente.
En la ordenación por combinación, la matriz que se va a ordenar se divide repetidamente en subarreglos hasta que cada subarreglo consta de un solo número. El algoritmo recursivo luego fusiona repetidamente los subarreglos y ordena el arreglo.
3. Clasificación rápida
Quicksort es otro algoritmo de clasificación basado en la técnica de programación Divide and Conquer. En este algoritmo, primero se elige un elemento como pivote y luego se divide la matriz completa alrededor de este pivote.
Como probablemente habrá adivinado, un buen pivote es crucial para una clasificación eficiente. El pivote puede ser un elemento aleatorio, el elemento multimedia, el primer elemento o incluso el último elemento.
Las implementaciones de ordenación rápida a menudo difieren en la forma en que eligen un pivote. En el caso medio, la ordenación rápida clasificará una matriz grande con un buen pivote en solo O (nlogn) tiempo.
El pseudocódigo general de quicksort divide repetidamente la matriz en el pivote y la coloca en la posición correcta de la submatriz. También coloca los elementos más pequeños que el pivote a su izquierda y los elementos más grandes que el pivote a su derecha.
4. Primera búsqueda en profundidad
Depth First Search (DFS) es uno de los primeros algoritmos de gráficos que se enseñan a los estudiantes. DFS es un algoritmo eficiente que se utiliza para recorrer o buscar un gráfico. También se puede modificar para usarlo en el recorrido del árbol.
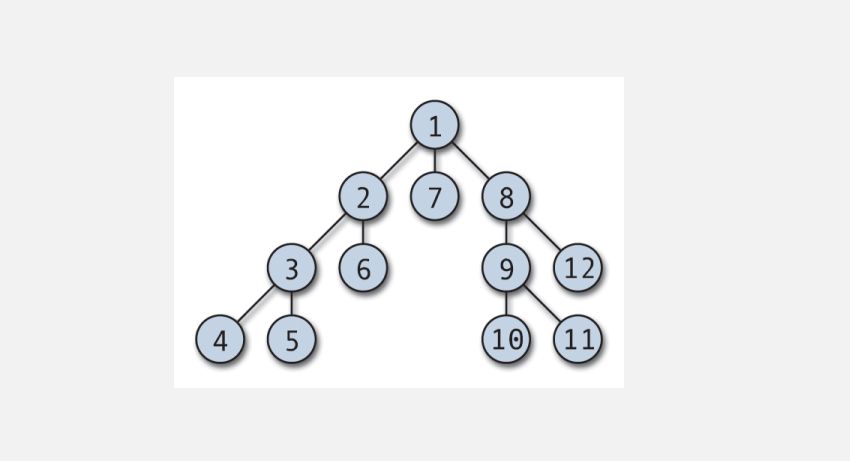
El recorrido DFS puede comenzar desde cualquier nodo arbitrario y se sumerge en cada vértice adyacente. El algoritmo retrocede cuando no hay vértices no visitados o hay un callejón sin salida. DFS generalmente se implementa con una pila y una matriz booleana para realizar un seguimiento de los nodos visitados. DFS es simple de implementar y excepcionalmente eficiente; funciona (V + E), donde V es el número de vértices y E es el número de aristas.
Las aplicaciones típicas del recorrido DFS incluyen la clasificación topológica, la detección de ciclos en un gráfico, la búsqueda de rutas y la búsqueda de componentes fuertemente conectados.
5. Búsqueda primero en amplitud
La búsqueda primero en amplitud (BFS) también se conoce como un recorrido de orden de nivel para árboles. BFS funciona en O (V + E) de forma similar a un algoritmo DFS. Sin embargo, BFS usa una cola en lugar de la pila. DFS se sumerge en el gráfico, mientras que BFS atraviesa el gráfico a lo ancho.
El algoritmo BFS utiliza una cola para realizar un seguimiento de los vértices. Los vértices adyacentes no visitados se visitan, se marcan y se ponen en cola. Si el vértice no tiene ningún vértice adyacente, se elimina un vértice de la cola y se explora.
BFS se usa comúnmente en redes peer-to-peer, la ruta más corta de un gráfico no ponderado y para encontrar el árbol de expansión mínimo.
6. Búsqueda binaria
La búsqueda binaria es un algoritmo simple para encontrar el elemento requerido en una matriz ordenada. Funciona dividiendo repetidamente la matriz por la mitad. Si el elemento requerido es más pequeño que el elemento del medio, entonces el lado izquierdo del elemento del medio se procesa más; de lo contrario, el lado derecho se divide por la mitad y se busca de nuevo. El proceso se repite hasta que se encuentra el elemento requerido.
La complejidad de tiempo de la búsqueda binaria en el peor de los casos es O (logn), lo que la hace muy eficiente en la búsqueda de matrices lineales.
7. Algoritmos mínimos del árbol de expansión
Un árbol de expansión mínimo (MST) de un gráfico tiene el costo mínimo entre todos los árboles de expansión posibles. El costo de un árbol de expansión depende del peso de sus bordes. Es importante tener en cuenta que puede haber más de un árbol de expansión mínimo. Hay dos algoritmos principales de MST, a saber, el de Kruskal y el de Prim.
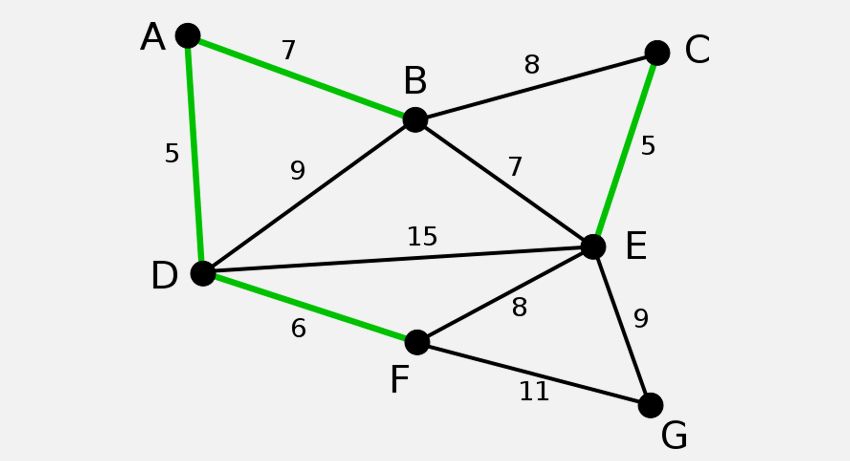
El algoritmo de Kruskal crea el MST agregando la ventaja con un costo mínimo a un conjunto en crecimiento. El algoritmo primero ordena los bordes por su peso y luego agrega bordes al MST comenzando desde el mínimo.
Es importante tener en cuenta que el algoritmo no agrega bordes que forman un ciclo. Se prefiere el algoritmo de Kruskal para gráficos dispersos.
El algoritmo de Prim también utiliza una propiedad codiciosa y es ideal para gráficos densos. La idea central en el MST de Prim es tener dos conjuntos distintos de vértices; un conjunto contiene el MST en crecimiento, mientras que el otro contiene vértices no utilizados. En cada iteración, se selecciona el borde de peso mínimo que conectará los dos conjuntos.
Los algoritmos mínimos de árbol de expansión son esenciales para el análisis de conglomerados, la taxonomía y las redes de transmisión.
Un programador eficiente es competente con algoritmos
Los programadores aprenden y desarrollan constantemente sus habilidades, y hay algunos elementos básicos esenciales en los que todos deben dominar. Un programador experto conoce los diferentes algoritmos, los beneficios e inconvenientes de cada uno y qué algoritmo sería el más apropiado para un escenario dado.
